0%

数据结构-数组-树-队列

发表于 2020-11-08 更新于 2024-08-12 分类于笔记阅读次数： Valine：

本文主要介绍了数据结构中的数组、树、队列的相关知识。

数组

参考文章

计算元素地址（i、j 均开始于 1）

主要是要分析出该元素前面有多少个(记为 n)元素，分析出来了即可知道下标为 n，LOC(i)=LOC(0)+size(L)*n。
分析过程：以行序或列序优先将矩阵中的元素依次排列。以按行序优先排列为例，假设 k 元素在第 i 行，则前面应至少有 x 个元素，再假设 k 在第 j 列，在当前行中前面应再有 y 个元素，从而得到 k 元素与 i、j 的对应关系。

按列序存放（高下标优先）

对于 A_m*n，有 LOC(i,j)=LOC(0,0)+(j*m+i)*sizeof(L)。
对于 A_abc，有 LOC(i,j,k)=LOC(0,0)+(k*a*b+j*a+i)*sizeof(L)。
同理可推至 n 维数组。

树

参考文章

树

非线性，一对多。（定义是递归形式的）
根（根结点的层为 1）、根的子树、结点的度（结点的子树数目）、叶子结点（也叫终端节点）、分支节点、双亲（虽然叫双亲但是 parent 只有一个）、树的深度（又称高度，叶子结点的层数）、兄弟、堂兄弟（同层不同双亲的结点）、祖先、子孙（所有子树的结点）、有序树（子树的顺序从左到右有限定，更换则不是同一颗树）、无序树。
森林：m 棵互不相交的数的集合，如 F={T₁,T₂,T₃}，任何一棵非空树可表示为 Tree=(root,F)，F 是子树森林。

因为 root 根结点被拆掉了之后剩下的子树就散了互不相交可以看作森林）

二叉树

递归定义：根节点，左子树右子树。每个结点的孩子是不会重复的。
每个结点至多两个子树，是有序树。
叶子结点的个数 n₀=度为 2 的结点数 n₂+1。（不直观，需要记）

总数 n=n₀+n₁+n₂，孩子的个数=n-1=2n₂+n₁。

含有 n 个结点的二叉链表中，有 n+1 个空链域。

利用 n₀=n₂+1，空链域数=2n₀+n₁。

满二叉树：深度为 k 且有 2^k-1 个结点的二叉树。

完全二叉树

每个结点都和同深度的满二叉树中的编号从 1 至 n 的结点一一对应。其叶结点只可能出现在层次最大或者第二大的层上。结点数 2^k-1-1<n<=2^k。
对于完全二叉树的第 i 个结点，若 2i>n，则该结点没有左孩子结点；若 2i+1>n，则该结点没有右孩子结点。若结点有双亲结点，则双亲结点的编号必然是 i/2 向下取整。

存储结构

采用链式存储结构比较方便。
三叉链表比二叉链表多一个指向双亲结点的指针。
静态链表也可以用来描述二叉树，此时的左孩子右孩子指针只要是孩子结点对应的标号（当然也可以是指针，但没必要）就可以了，整体看起来是一个结构数组。

二叉树遍历：

D----访问根节点，输出根节点
L----递归遍历左子树
R----递归遍历右子树

先序遍历 DLR
中序遍历 LDR
后序遍历 LRD

队列

参考文章

总结

队列遵循 FIFO 原则，但是不一定以 FIFO 的方式排序各个元素。

非循环队列

数据迁移只需要在 tail=MaxSize&&head!=0 时进行，以节省使用代价。
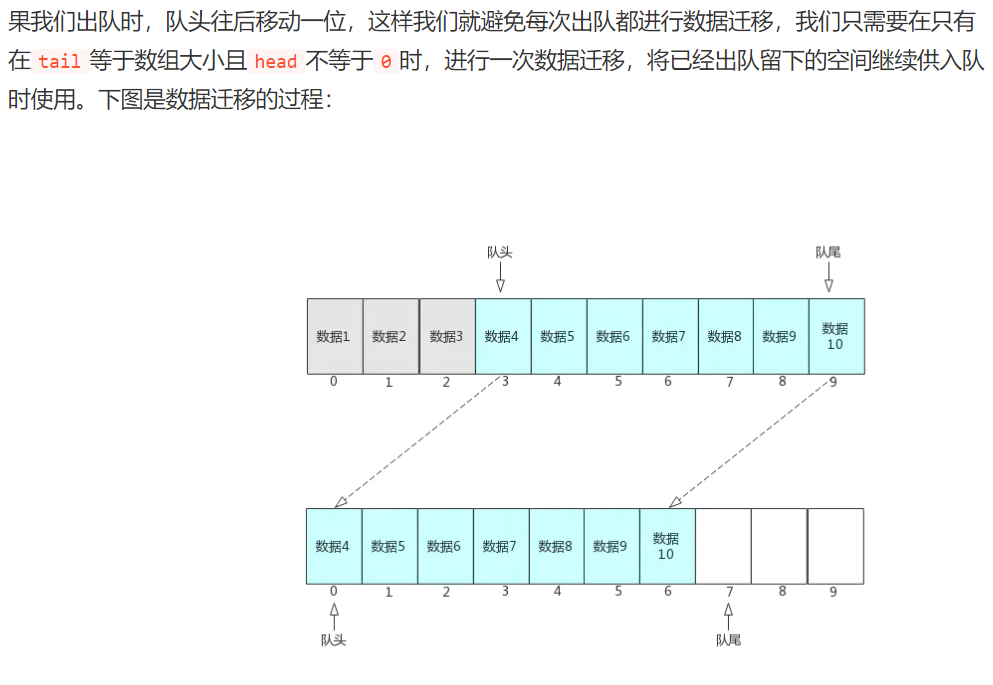
判断队列满了的条件，tail = MaxSize,head = 0。
链式队列与顺序队列比起来不需要进行数据的迁移，实现相对简单很多，但是链式队列增加了存储成本。

循环队列

对于一个存储空间为 n 的循环队列，只能存放 n-1 位数据，令 tail 与 head 重合时为队空条件，(tail+1)%MaxSize==head 时为队满条件。
出入队列都应该取模。比如入队 tail=(tail+1)%MaxSize，出队 head=(head+1)%MaxSize。
队列长度 length=(tail-head+MaxSize)%MaxSize。一般队列长度仅需要 tail-head，而循环队列中，head 可能会比 tail 大，所以需要加上 MaxSize 并取模。
由长度公式以及队满条件知，显然，循环队列队满时 length 为 MaxSize-1。

双端队列（Deque）

队头、队尾都可以进行入队、出队操作。总之它即有栈的功能，也有队列的功能。
在将双端队列用作队列时，将得到 FIFO 行为；在将双端队列用作堆栈时，将得到 LIFO 行为；

优先队列（不遵循 FIFO）

从队头出队，队尾入队。不过每次入队时，都会按照入队数据项的关键值进行排序。保证优先级最高的最先出队。
一般用堆实现。